算法21：折纸问题

请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。此时折痕是凹下去的，即折痕突起的方向指向纸条的背面。 如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。

给定一个输入参数N，代表纸条都从下边向上方连续对折N次。 请从上到下打印所有折痕的方向。

例如:N=1时，打印: down N=2时，打印: down down up

根据题目要求，我实际折了一把，并且每一次折的时候，我都进行了标注：1凹，代表第一次折的， 2 凹或者2凸代表第二次折的，依次类推…..

观察了上图，确实停迷惑人的，下图我通过绘图的形式，更加直观的呈现这个问题的本身

通过手动绘制的图片，我们按照折纸的先后顺序，发现每次折纸，都会在之前的折纸痕迹左右再生出2道痕迹：

第一次折： 1 凹

第二次折： 1 凹两侧生出了 2凹 和 2凸

第三次折: 2凹 和 2凸两侧又生成了 3凹 和 3 凸

依次类推………

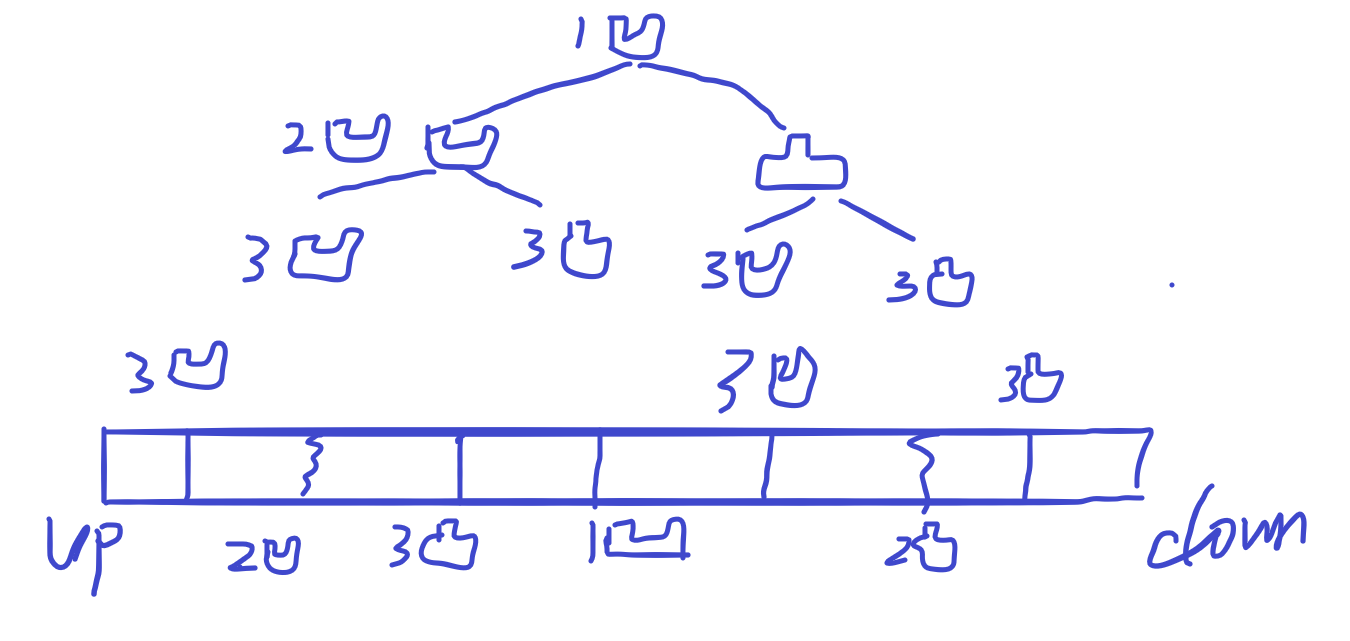
最终我们发现，这就是一颗满二叉树。而想要从上到下打印这张纸的痕迹，实际上就是中序遍历整颗二叉树的节点。代码如下

package code03.二叉树_02;

/**
 * 请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。此时折痕是凹下去的，即折痕突起的方向指向纸条的背面。
 *
 * 如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。
 *
 * 给定一个输入参数N，代表纸条都从下边向上方连续对折N次。 请从上到下打印所有折痕的方向。
 *
 * 例如:N=1时，打印: down N=2时，打印: down down up
 */
public class Code03_PaperTree {

    /**
     * @param times 代表折了几次纸，也代表二叉树的层数
     * @param n     代表二叉树的层数
     * @param down  凹代表true，凸代表false
     */
    public void process (int times, int curTimes, boolean down)
    {
        //上一层已经是最下方的层数，没有下挂节点了
        if (curTimes > times) {
            return;
        }
        //根据观察，每一层的左节点都是凹
        process(times, curTimes + 1, true);
        System.out.print(down ? "down " : "up ");
        //每一层的右节点都是凸
        process(times, curTimes + 1, false);
    }

    public void paperOut (int times)
    {
        //times小于1，代表没折纸
        if (times < 1) {
            return;
        }

        //系统记录折纸的次数, 用来与times作比较用
        int curTimes = 1;
        //第一次默认是凹下去的
        process(times, curTimes, true);
    }

    public static void main(String[] args) {
        Code03_PaperTree test = new Code03_PaperTree();
        int times = 2; //折纸次数
        test.paperOut(times);
    }
}